Recursion is a process by which a function calls itself repeatedly, until some specified condition has been satisfied.
- In order to solve a problem recursively, two conditions must be satisfied. First, the problem must be written in a recursive form, and second, the problem statement must include a stopping condition.
Factorial Program using loop in java
|
1 2 3 4 5 6 7 8 9 10 |
class FactorialExample{ public static void main(String args[]){ int i,fact=1; int number=5;//It is the number to calculate factorial for(i=1;i<=number;i++){ fact=fact*i; } System.out.println("Factorial of "+number+" is: "+fact); } } |
Factorial Program using recursion in java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class FactorialExample2{ static int factorial(int n){ if (n == 0) return 1; else return(n * factorial(n-1)); } public static void main(String args[]){ int i,fact=1; int number=4;//It is the number to calculate factorial fact = factorial(number); System.out.println("Factorial of "+number+" is: "+fact); } } |
Application Area of Recursion
Method Calls & Recursion implementation
Differences between recursion and iteration:
- Both involve repetition.
- Both involve a termination test.
- Both can occur infinitely.
| Iteration | Recursion |
| Iteration explicitly user a repetition structure. | Recursion achieves repetition through repeated function calls. |
| Iteration terminates when the loop continuation. | Recursion terminates when a base case is recognized. |
| Iteration keeps modifying the counter until the loop continuation condition fails. | Recursion keeps producing simple versions of the original problem until the base case is reached. |
| Iteration normally occurs within a loop so the extra memory assigned is omitted. | Recursion causes another copy of the function and hence a considerable memory space’s occupied. |
| It reduces the processor’s operating time. | It increases the processor’s operating time. |
Anatomy of a Recursive call
The function that defines raising any number x to a nonnegative integer power n is a good example of a recursive function. The most natural definition of this function is given by:
Using this definition, the value of x4 can be computed in the following way:
x4 = x · x3 = x · (x · x2) = x · (x · (x · x1)) = x · (x · (x · (x · x0)))
= x · (x · (x · (x · 1))) = x · (x · (x · (x))) = x · (x · (x · x))
= x · (x · x · x) = x · x · x · x
Tail Recursion
A recursive function is said to be tail recursive if there are no pending operations to be performed on return from a recursive call.Tail recursion is also used to return the value of the last recursive call as the value of the function.Tail recursion is advantageous as the amount of information which must be stored during computation is independent of the number of recursive calls.
It is tail recursive
|
1 2 3 4 5 |
void tail(int i) { if (i>0) { system.out.print(i+"") tail(i-1) } |
Is the factorial method a tail recursive method?
|
1 2 3 4 5 6 |
int fact(int x){ if (x==0) return 1; else return x*fact(x-1); } |
When returning back from a recursive call, there is still one pending operation, multiplication. Therefore, factorial is a non-tail recursive method.
Advantage of Tail Recursive Method
Tail Recursive methods are easy to convert to iterative.
|
1 2 3 4 5 6 |
void tail(int i){ if (i>0) { system.out.println(i+""); tail(i-1) } } |
>>>>
|
1 2 3 4 |
void iterative(int i){ for (;i>0;i--) System.out.println(i+""); } |
- Smart compilers can detect tail recursion and convert it to iterative to optimize code
- Used to implement loops in languages that do not support loop structures explicitly (e.g. prolog)
Indirect Recursion
- If X makes a recursive call to X itself, it is called direct recursion.
- Indirect recursive methods call themselves indirectly through calling other methods.
- In general, indirect recursion is a circular sequence of two or more recursive calls: X1 –> X2 –> … –> X1.
Indirect Recursion Example
Three method for decoding information are:
- receive: stores information in buffer and calls decode.
- decode: converts information to new form and calls store
- store : stored information in a file, call receive.
We have a chain of calls: recieve() -> decode() -> store() ->recieve()-> decode()….
Nested Recursion



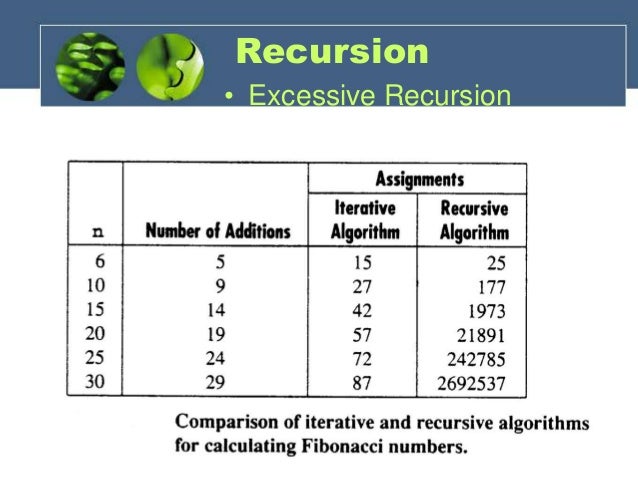
Excessive Recursion


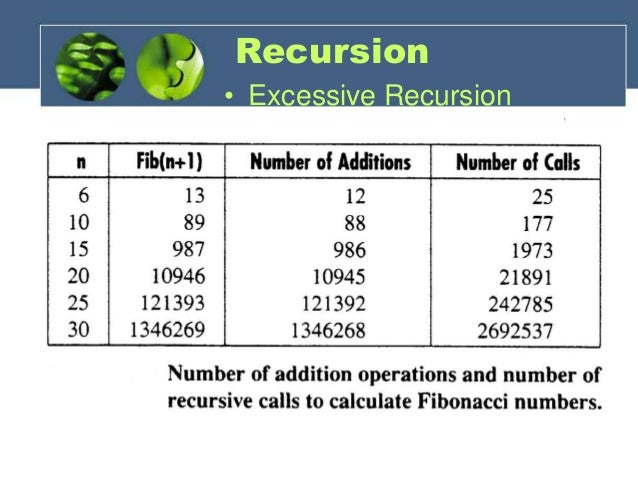
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
void IterativeFib(int n) { if (n < 2) return n; else { int i = 2, tmp, current = 1, last = 0; for ( ; i<=n; ++i) { tmp= current; current += last; last = tmp; } return current; } } |

Backtracking
History
- Backtrack’ the Word was first introduced by Dr. D.H. Lehmer in 1950s.
- R.J Walker Was the First man who gave algorithmic description in 1960.
- Later developed by S. Golamb and L. Baumert.
Definition:-
Backtracking is a methodical way of trying out various sequences of decisions, until you find one that “works. Backtracking allows us to systematically try all available avenues from a certain point after some of them lead to nowhere. Using backtracking, we can always return to a position which offers other possibilities for successfully solving the problem.
Advantages
- Comparison with the Dynamic Programming, Backtracking Approach is more effective in some cases.
- Backtracking Algorithm is the best option for solving tactical problem.
- Also Backtracking is effective for constraint satisfaction problem.
- In greedy Algorithm, getting the Global Optimal Solution is a long procedure and depends on user statements but in Backtracking It Can Easily getable.
- Backtracking technique is simple to implement and easy to code.
- Different states are stored into stack so that the data or Info can be usable anytime.
- –The accuracy is granted.
Disadvantages
- Backtracking Approach is not efficient for solving strategic Problem.
- The overall runtime of Backtracking Algorithm is normally slow
- To solve Large Problem Sometime it needs to take the help of other techniques like Branch and bound.
- Need Large amount of memory space for storing different state function in the stack for big problem.
- Thrashing is one of the main problem of Backtracking.
- The Basic Approach Detects the conflicts too late.
–
Application of Backtracking
- Optimization and tactical problems
- Constraints Satisfaction Problem
- Electrical Engineering
- Robotics
- Artificial Intelligence
- Genetic and bioinformatics Algorithm
- Materials Engineering
- Network Communication
- Solving puzzles and path
Some Problem Solved with Backtracking Technique
- N- Queens Problem
- Sum of Subset
- Sudoku Puzzle
- Maze Generation
- Hamiltonian Cycle
8-Queens Problem
History:
First Introduced in 1848 which was known as 8- queens Puzzle. Surprisingly, The First Solution was created in 1950 by Franz Nauck. Nauck made an 8X8 Chessboard to find the first Feasible Solution.
![A solution to the 8-queens problem, presented as [5, 1, 8, 4, 2, 7, 3, 6].Â](https://www.researchgate.net/profile/Ellips_Masehian/publication/257549155/figure/fig1/AS:297614982565906@1447968349895/A-solution-to-the-8-queens-problem-presented-as-5-1-8-4-2-7-3-6.png)
Problem Description
In a NxN square board N – number of queens need to be placed considering three Condition —
- No two Queens can be placed in same row.
- No two Queens Can be places in same Column
- No two queens Can be placed in same Diagonal.
